Activation Functions

Activation functions define the output of a graph node given a set of inputs, as illustrated below. Activation functions:

provide the capability to introduce non-linearity in order to model non-linear aspects of the real world
are monotonic - that is, they either constantly increase or decrease - this is important in neural network training to avoid chaotic behavior

Activation Functions commonly used in Machine Learning include:

Activation Function Generalized Equation

An activation function receives the sum of inputs which are modified by weights and a bias, modifies the input sum and produces an output. During neural network training, the weights and bias are repeatedly modified in order to produce a neural network result that has a minimal error (loss) compared to observed training examples.

Using:
   b = bias
   a = value passed in from another node
   w = weight to be applied to the value
   s = sum of the weighted values and the bias
   g = activation function applied to the sum
   t = output values sent to other nodes

$\left.\begin{matrix}b\, \, \: \rightarrow \\ a _{1}\rightarrow \\w _{1}\rightarrow \\ \vdots \\ a _{n}\rightarrow \\ w _{n}\rightarrow \end{matrix}\right\} \rightarrow \left [ s=\sum_{i=1}^{n}w_{i} a_{i}+b\right ] \rightarrow g\left ( s \right )\rightarrow \left\{\begin{matrix}t_{1}\rightarrow \\ \vdots \\ t_{m}\rightarrow \end{matrix}\right.$

In an Artificial Neural Network, Activation Function nodes are positioned between input and output nodes:

and the flow of data through nodes looks like this:

Activation Function Example from Nature

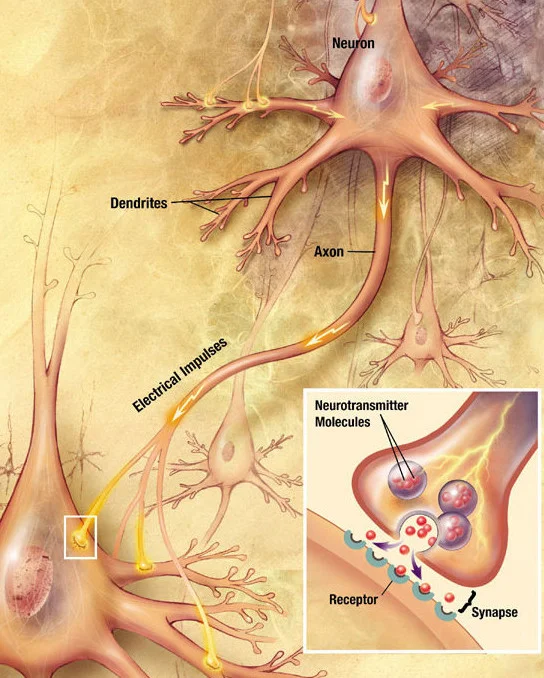
Activation functions are modeled on biological brain and other body cells.

One example is the shift in the action potential of a brain cell. Brain neurons and axons activate and carry electrical signals via neurotransmitter molecules:

BY USER:LOOIE496 CREATED FILE, US NATIONAL INSTITUTES OF HEALTH, NATIONAL INSTITUTE ON AGING CREATED ORIGINAL - HTTP://WWW.NIA.NIH.GOV/ALZHEIMERS/PUBLICATION/ALZHEIMERS-DISEASE-UNRAVELING-MYSTERY/PREFACE, PUBLIC DOMAIN, HTTPS://COMMONS.WIKIMEDIA.ORG/W/INDEX.PHP?CURID=8882110

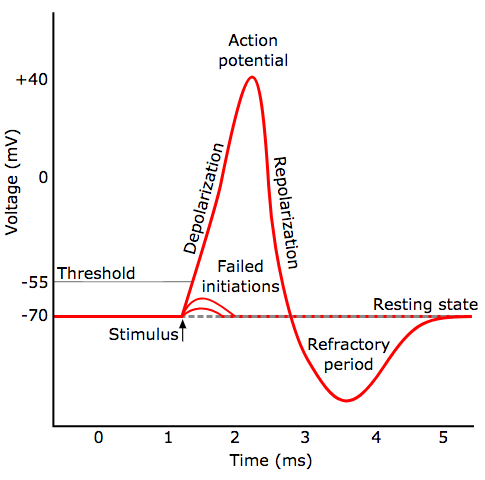
The voltage of a signal over time looks like this:

By Original by en:User:Chris 73, updated by en:User:Diberri, converted to SVG by tiZom - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2241513

Activation Functions

Activation Function Generalized Equation

Activation Function Example from Nature

References